• • •
"Mike and Jon, Jon and Mike—I've known them both for years, and, clearly, one of them is very funny. As for the other: truly one of the great hangers-on of our time."—Steve Bodow, head writer, The Daily Show
•
"Who can really judge what's funny? If humor is a subjective medium, then can there be something that is really and truly hilarious? Me. This book."—Daniel Handler, author, Adverbs, and personal representative of Lemony Snicket
•
"The good news: I thought Our Kampf was consistently hilarious. The bad news: I’m the guy who wrote Monkeybone."—Sam Hamm, screenwriter, Batman, Batman Returns, and Homecoming
April 24, 2011
Fishy Statistics
By: Aaron Datesman
Scientists like to reason by analogy. Possibly this is because they're lazy, which is sometimes true, and possibly this is just an idea that the SAT puts into their heads at a young age and which they are never able to shake. However, possibly it's also because the mathematical framework which the natural world obeys is universal. Because of this, sometimes it happens that what you know about one field of inquiry turns out to apply in a very different area.
Until recently, my professional field was the construction of astronomical receivers: specifically, detectors utilizing sensitive superconducting electronics. Similar to radioactive decay probabilities, the design of sensitive receivers requires the careful analysis of stochastic (random) effects. Perhaps this seems new to you, but it isn't - you most likely learned to call it "noise".
To give one concrete example, the sound you hear when you mis-tune an analog radio and turn the volume up is the result of statistical fluctuations in electron states. Statistical effects like those of the thought experiment in the last two posts are not abstract in the least - they are highly present in the everyday world and have significant practical impact. Statistical fluctuations in the density of air explain why the sky is blue, for instance.
One of the noise sources for which an astronomer must account when devising an observing strategy is known as shot noise. Fundamentally, shot noise in electrical circuits arises because electrical current comes in discrete packets called "electrons". If the average flow of current in a wire is 4 electrons in a given unit of time, it's quite likely that some intervals witness 2 electrons passing by, others 5, or 7, etc. This statistical variation limits the ultimate sensitivity of the receiver.
Radioactive decays also occur in discrete units - of single nuclei. Therefore, it should be no surprise that the same statistical rule governing shot noise also describes radioactive decay. Although I think it has nothing to do with fish, the relationship is known as Poisson statistics. For radioactive decay, the Poisson distribution relates the probability that N decays occur in a given volume in a given time (say, in one cubic meter in one second) to the average decay rate, N-bar:
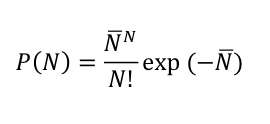
Let me illustrate with an example. This post about the Science article "Radioactive Plume from the Three Mile Island Accident: Xenon-133 in Air at a Distance of 375 Kilometers" noted that the air in Albany, NY, contained about 10 pCi/m^3 of Kr-85 from 1975 to 1979. This equates to about 1 decay per second in a volume of 1 cubic meter. One per second (1/sec) is the average decay rate, N-bar.
We can use the equation at the bottom of this post, along with the information that the half-life of Kr-85 is 10.76 years, to determine that a cubic meter of atmosphere with an average decay rate of one nucleus per second contains more than one billion atoms of Kr-85. This isn't a lot, as far as numbers of atoms go (it isn't even one part in one trillion), but it does represent a large reservoir from which more decays could occur in a given one second interval. Nevertheless, only the average decay rate in the volume contributes to the probability expression.
So, it's interesting to ask questions like this one: how likely am I to see 10 decays in one second in this volume of 1 cubic meter, rather than just the average rate of 1 decay per second? The probability is 10^-7, or 0.00001%. This is a small number, but there are a lot of cubic meters in the atmosphere, and a lot of seconds in a year. Somewhere, at some time, you are virtually certain to observe a decay rate of 10 per second - and even, once in a long while, much larger values.
(Just to show how the decay probability falls off with increasing N, the probability for 2 decays per second is 18% - six orders of magnitude larger.)
Over a large volume of many cubic meters and a long time, the number of decays must agree with the average decay rate. I feel it's important to understand, however, that large numbers of simultaneous decays absolutely must occur in individual volumes of one cubic meter somewhere at some time. The fundamental distinction is identical to the difference between instantaneous and average velocity, with which every student of Introductory Physics should be familiar.
Because a cancer five or twenty years down the road began originally in a single cell (or perhaps in a small group of cells), in my opinion it's clearly preposterous to relate health outcomes to whole-body doses calculated from an average decay rate. Due to statistical mechanics, the dose delivered to an individual cell can be MANY, MANY times higher than the average dose - rather counter-intuitively, if the average dose is low. This is basic undergraduate physics, and not at all open to dispute.
What is actually required is a statistical treatment relating the occurrence of high-dose disintegrations to the background rate. I am confident that the correct statistical treatment will show that it is entirely improper to estimate the health effects of low doses by linear extrapolation from high doses.
In which case, I have to ask: wouldn't it be better if the people telling us that small amounts of radiation aren't harmful had taken, you know, undergraduate physics?
— Aaron Datesman
Posted at April 24, 2011 09:55 AMQ.E.D.
Posted by: Amandasaurus at April 24, 2011 10:35 AMOK, I've taken first-year physics. I've even taught physics, albeit to MCAT prep students.
In the post you link back to, "Not a Super Model", you're not claiming that there's no absolutely safe lower dose of radiation (which isn't controversial), but that lower doses of radiation are actual MORE harmful than higher doses. That's simply not the case. There's lots of good evidence that people who have suffered greater exposures are more likely to develop cancer or otherwise suffer harm than those who've suffered lower exposures.
And by your argument here, statistically speaking, you'll be even more likely to have a higher instantaneous dose (using the example of 10 decays per second in a single cubic meter) if the average dose is higher. Using your own math, if the air in Albany from 1975-79 had contained 100pCi/m^3 of K-85 (100, not 10, a 10-fold increase), the average dose would then be 10 decays per second per cubic meter (which is your worst case scenario if the average dose is actually 1 decay per second per cubic meter -- statistically improbable but sure to occur at least sometime, somewhere). If the average dose is 10, then you'd have the same low odds (1 in 10^7) of having an instantaneous dose of 100 decays in a given second in a given cubic meter. Which would be more radiation, and that much more likely to trigger cancer in a given cell (in part because any given cell might get more radiation, but mostly because more cells -- there are a lot of cells in a cubic meter -- would be exposed).
You can make the same argument for any carcinogenic factor, or even any exogenous disease causing factor.
UV radiation from the sun can trigger melanoma in a melanocyte. The amount of local radiation to a given cell has a stochastic element, and will vary around a mean. You never know, even in low-UV situations, one particular melanocyte might be unlucky enough to receive an improbable-but-still-possible harmful dose of UV, and start undergoing neoplastic changes.
Washing the hands removes most of the bacteria on them, but not all. Even with careful and frequent handwashing, it's still quite possible (though comparatively unlikely) that a particular bacterium will survive on the skin and get introduced into a vulnerable site, causing infection. There might not be that many bacteria on the hand in total (average dose), but one in the wrong spot (instantaneous dose) might still cause disease.
But that doesn't mean that washed hands aren't cleaner than non-washed, and comparatively less likely to trigger bacterial infections. Nor that lower UV exposures aren't less likely to cause melanoma than higher UV exposures. Nor that lower doses of ionizing radiation from nuclear power plant disasters aren't less likely to cause harm than higher doses.
In all cases, there's no threshold beyond which exposure is perfectly, absolutely safe in all cases at all times. In all cases though, risk is LOWER in low-dose exposures, meaning fewer people (cells, sure) are exposed to a given dose less often than if doses are higher. That's what risk means.
But low risk doesn't mean zero harm is possible, just like the powerball winner might be the guy who bought his first-ever lottery ticket that week, and not the guy who's been buying 50 tickets a week for years now. The guy with 50 tickets still has a higher CHANCE of winning, even if the guy with a single ticket is actually lucky enough to win the lottery.
The trick is (and you're free to claim this is sleight of hand), beyond a certain level of low risk, it's generally not reasonable to either worry about harm (on an individual level) or prevent harm (on a societal/institutional level). I have a risk of being hit by a meteorite when I take my kids to the park this afternoon. The risk of that (based on the yearly "average dose" of celestial objects crashing to earth) is low, but if I'm unlucky enough to catch a falling star to the back of the head this afternoon (instantaneous dose), I won't be any less dead. I might also get melanoma from the sun hitting one of the moles on my neck or get hemorrhagic colitis from an E coli from a puddle near the swingset, who knows. I could get hit by a drunk driver or shot by a kid playing with his uncle's shotgun or I could inhale some farflung particle from Fukushima and develop lung cancer 3 years from now. The thing is, while none of those risks are zero (and therefore absolutely safe), none of them are high enough that I'm worried about them.
And you can say, and should say in my opinion, that nuclear power and its associated disasters are more preventable than UV from sunlight or coliform bacteria from the soil, because it's a human venture and we could stop it or change course to at least try to make it much safer even at the expense of efficiency or a lower price.
And that's a good point, but then you're back in epidemiology (where you seem to have very little experience), arguing about risk vs benefit of the entirety of human existence. What causes more harm, nuclear power or coal power? Nuclear power or smoking? Nuclear power or drinking alcohol? Nuclear power or firearms? What among these modifiable risks is most amenable to change or control at the level of a society (taxes, prohibition, regulation, etc). And there's no equation that answers those questions, because they're political and social and medical questions, not physics.
Posted by: pmpm at April 24, 2011 01:07 PMAlso, while it's true that a single cell that becomes cancerous is likely to be exposed much more than an average cell, there is a statistical fallacy involved in looking at those cells first: then you are looking at an extreme value distribution - you're picking out the worst-case and then treating it as an average case, statistically. Also, it doesn't make sense to compare an individual cell's exposure to the average exposure amount - what's important is comparing the number of events in the individual cell (even the worst case) to the background exposure amount, and this goes up no matter what the more radiation exposure you have.
Posted by: saurabh at April 24, 2011 02:11 PMpmpm
Maybe I've become confused, but I don't think Aaron has disputed that greater exposures can cause greater harm. As I understand him, he has claimed that the use of linear extrapolation to argue based on effects of high doses of radiation that low doses are safe ignores basic physics, which galls him the way it galls me to listen to people chortle about political conspiracies. Because I am ignorant of basic physics, I can't say whether he's right about the basic physics, but his point seems cogent to me. I believe that does not necessarily mean that low doses are in fact more dangerous than high doses, though he has suggested why they could be. I'm less sure of the latter point and am out of my depth here, and even if he's right, I suspect you're right that we're all constantly being killed by lots of things that industry and regulators pretend are safe. I guess that leads me in a different direction though.
Posted by: N E at April 24, 2011 05:30 PMI, too, am a little confused about what Aaron is trying to prove. I'll go by what NE says and assume he wants to debunk the linear model. I could imagine (as a sci-fi writer might) that a damaged cell could "diffuse" its harm to its neighbors in ways a saturated complex might not, in which case the resulting nonlinearity would work to the disadvantage of low-dose hits and Aaron might well be on his way to getting two Nobel prizes (medicine and peace).
But Aaron chose another line of attack, which is to prove that epidemiologists can't do statistics. I thought that's pretty much ALL they do, so that seems a bit harsh. But let's look at Aaron's argument. He focuses on large deviations. If you get hit on the nose by one tennis ball per match on average, then play for enough years and sure enough, one day, you'll get hit by 10 of them in a single match (after which your brain will explode because 10 is the brain explosion threshold). Note that if your average is not 1 per match but 2 then you'll get hit by 10 at some EARLIER point. Now I think Aaron asks: how much earlier? Aaron says more than half the time, which indeed would disprove the linear model (since doubling the hit rate would less than double the death rate). However, one quick look at Aaron's "fishy" expression shows that it's plainly false. So maybe Aaron misspoke and meant small deviations. While his point is definitely truer, one needs only a small correction to the linear coefficient to fix it. Bottom line, I see nothing wrong with the linear model from the statistics side. Supralinearity will require a biological analysis. (I failed to see why that would follow from Aaron's previous mystery graph -- the one with the green triangles -- but he never explained what all those green objects were, so who knows?)
Actually, the blue color of the sky is caused by Rayleigh scattering.
Other than that, I have no quarrel with your discussion of poisson statistics. But the balance of the evidence is that at very low doses radiation has a beneficial effect, through the biological phenomenon of hormesis.
Posted by: Jinzang at April 24, 2011 07:31 PMpmpm:
I think that Aaron is making both a scientific point, and a political one. If the dangers of nuclear power are not correctly explained to the public because of a misrepresentation of statistical variation, it is impossible to make a well-informed political decision. Given what I have learned about the uncertainty in our knowledge of the health effects from nuclear power from this series of posts, it has without a doubt influenced my political opinion towards it. Whether or not he has conclusively disproven linear extrapolation is irrelevant; he has certainly illustrated that the dangers of nuclear power, as presented, are too neat and tidy to be true to the extent that the general public believes in them.
Gordon: Thanks for making that point. What I take from this series of posts is the terrifying amount of uncertainty about a technology that can be potentially catastrophic. It seems that experts are all over the map in their assurances of this or that. For that alone, we all owe Aaron a big debt of gratitude.
A few things:
1) We have ignorance over the health effects of radiation but we also have ignorance over the health effects of chemical and biological agents for much the same root reasons. We look back 50 years ago and are appalled by some practices and in 50 years we will be appalled by some of our practices today. Decreasing ignorance is important but, as far as political decisions go, they must be made as best is possible given the state of ignorance. Ignorance should be a factor in a decision making process and not an impediment.
2) There is a difference between claiming that extreme effects are a bigger relative consideration at low doses then it is at high doses and claiming that low doses pose a greater risk. I believe that the later has not been claimed. I believe that Mr. Aaron is still contending that there is a monotonic relationship between risk and dose but the relationship is not linear and risk is greater then a linear relationship would warrant.
3) The argument presented in this post is that with a per cell average of n absorptions in the body, there is a greater chance for a single cell to absorb at least r*n itself for a lower n with r>1 being constant. If the Poisson distribution models the distribution of the amount each cell absorbs with a given per cell average is true, the argument is true. I am not smart enough to critique the argument that a Poisson distribution is correct with authority but the argument makes sense to me.
4) The argument in the post is sufficient but not necessary to argue that the linear dosing model of extrapolating an affine ("linear" as it is popularly used) fit for high doses to low doses underestimates the harm at low doses. Other arguments have been disused in previous posts and their comment sections.
5) My discussion above should in no way be a claim that the entire point and arguments of the post is limited to what I discussed here. I only talked about a small part of it in detail. There is a problem with two parts: what does is delivered to the body and once it is delivered, what happens?
Posted by: Benjamin Arthur Schwab at April 24, 2011 09:00 PMJinzang
I'm a little skeptical that there is a balance of evidence in favor of radiation hormesis. As an expert reader of wikipedia, i see that even leading nuclear bodies do not yet accept radiation hormesis, and I would think the nuclear industry would favor that theory with the same enthusiasm that energy companies have shown for propounding cockamamie climate change hypotheses. If they aren't even behind it, there can't possibly be a balance of evidence for it.
Posted by: N E at April 24, 2011 09:03 PM"We look back 50 years ago and are appalled by some practices and in 50 years we will be appalled by some of our practices today. Decreasing ignorance is important but, as far as political decisions go, they must be made as best is possible given the state of ignorance."
There is an important element of propaganda embodied in the above statement. I strongly disagree that decreasing ignorance is the paramount issue, though that view is pumped into us nonstop by corporate advertising and lobbying. Many of the appalling practices of the past were pretty well understood to be appalling at the time, but they could be gotten away with. It was not so much a matter of ignorance as lack of accountability pared with immorality fed by greed and cynicism about ideals. Doing things that kills workers or consumers or others is easily rationalized in business environments. Not so many people will look you in the eye and cut your throat, but it's commonplace to murder anonymous people by exposing them to this or that or having them do something likely to be lethal. The fact that people who do not work for Enron or in other proudly amoral firms still around often do not like to be extremely honest with themselves about this does not mean they don't know what they are doing. They know, but moral responsibility dissipates much more quickly than ionizing radiation, and even the slightest wind will blow it away.
Posted by: N E at April 24, 2011 10:31 PMObviously NOBODY really knows. As luck would have it, (with the tremendous efforts of the good folks at GE)WE have a wonderful opportunity to study this question of low/high dose affect. WE have a DENSE population of highly educated and knowledgeable people EXPERIENCED in the effects of radiation in their environment. In OUR test case there are accurate measurable population groups at various distances from the source of contamination. I'm SURE these people will keep accurate records of contamination levels and health cases, if for no other reason than the soon to occur lawsuits. The density of the population may well help to remove any ambiguities in the data retrieved. OUR experiment WILL last a long, long time, so, if WE are dilligent WE can find OUR answers. Time will tell.
Posted by: Mike Meyer at April 24, 2011 11:39 PM@N E
In the post he linked to at the end of this one, titled Not A Super Model, Aaron somehow extrapolated from the fact that biological effects can be nonlinear to the conclusion that "it is plausible" that lower doses of radiation might be more harmful than higher doses.
He's wrong. It's not plausible.
Soon after that, he put up a post purporting to draw a link between worldwide total collective radiation dose and the incidence of cancer. Only he didn't notice that the table he drew his epidemiological numbers from for cancer incidence was actually listing cancer deaths, and he never accounted for the fact that most radiation-induced cancers take years to develop and many aren't fatal, and he cherry picked the starting point of the graph to exclude a huge run-up in the number of cancer deaths in the decades going back to 1900 not included on his graph, and he plotted a linear scale for deaths against an exponential one for radiation doses, as if that was the same thing.
I pointed out the errors. He didn't update the post to correct his "typo" confusing incidence rates with deaths, and maintained in comments that his graph was "approximately correct and certainly entirely defensible".
He's wrong. It was neither.
And now in this post he goes through some Poisson statistics just to point out that even unlikely events do happen, without pointing out that they don't happen very often, because they're unlikely. He seems to think the statistics he's presenting have something to do with physics, when they're just basic principles of MATH inherent in any risk/chance scenario.
It's maddening - I'm a political ally here and have read every post on this site since the beginning. I'm happy to support the politics that says that nuclear power should be better regulated, made more expensive, maybe even banned completely, or to say that powerful people have an interest in downplaying or even hiding bad things that have happened at Three Mile Island or any one of a number of other disasters.
But I don't think these politics require us to distort the actual numbers of risk/chance involved, or to misinterpret the epidemiological evidence, or otherwise make a bunch of earnest but misguided errors.
Aaron is pointing out that low doses of radiation can be "dangerous", where "dangerous" apparently means has a non-zero risk. But he never compares that risk to other unlikely events.
In this post he goes through a long explication to get to a risk of 1 in 10^7 that a given cubic meter of "low dose" radiation might actually give you a high dose in a given single second. Which is true, but what is the risk that I'll be occupying that space at that time?
You could compare that number to the single-year risk of being hit by lightning, 1 in 6.2 million. That sounds unlikely, but the odds are actually more likely than Aaron's 1 in 10^7 scenario.
But if you said, "low dose radiation is not zero risk, but the risk that it could be dramatically more harmful than expected in a given spot at a given time is somewhat less than the risk that you'll personally be struck by lightning in 2012", that wouldn't reinforce the narrative that we should all be scared.
Posted by: pmpm at April 25, 2011 12:08 AM@pmpm: to be fair to Aaron, a chance of 10^-7 per second means that it is likely to happen to you in a year if you live in the exposed area. So it's not like lightning. The problem with his argument is that higher doses increase that probability superlinearly, which means that lower doses are indeed, as intuition would have it, much better. I am not questioning Aaron's conclusion, which might well be correct: it's the way to get there I cannot follow.
I've been following this as best I can, and I find it fascinating, but my problem is that you throw a lot of hard-to-understand math at us, and a lot of "we don't know," when what I want is to see the risk as you see it quantified in some way that I can compare to other risks. My starting point is the very easy-to-understand graph of statistics created by the WHO, comparing worker deaths per terawatt hour from various energy sources.
Coal – world average 161 (26% of world energy, 50% of electricity)
Coal – China 278
Coal – USA 15
Oil 36 (36% of world energy)
Natural Gas 4 (21% of world energy)
Biofuel/Biomass 12
Peat 12
Solar (rooftop) 0.44 (less than 0.1% of world energy)
Wind 0.15 (less than 1% of world energy)
Hydro 0.10 (europe death rate, 2.2% of world energy)
Hydro - world including Banqiao) 1.4 (about 2500 TWh/yr and 171,000 Banqiao dead)
Nuclear 0.04 (5.9% of world energy)
So while I find it interesting to read all this arcane theorizing, it will take something more to reverse the impression of risk that these hard numbers provide.
Posted by: godoggo at April 25, 2011 02:11 AMIncidentally that was via this post, which I came upon via Sullivan a while back.
Mx. N E:
There is a difference between the people of Enron knowing what they're doing and the unsuspecting California electricity consumer knowing what Enron is doing. Once the public was made aware of how damaging DDT was it stooped being used. There were concerns over its use since the start but it was plausible to believe it was safe in the 40's and into the 50's. At some point the manufacturers probably knew how damaging it was and tried to hide it. This doesn't mean that county commissioner in Free County, USA, is being willfully ignorant in trying to make a decision on whether or not to permit DDT use in the late 50's. In this case it is important to decrease the ignorance of the public and the politicians but I'm not going to fault a county commissioner who is acting in good faith. The ignorance of the public is more important however. If a county commissioner were presented with the need to build a nuclear plant or a coal plant, it would still be reasonable to build the nuclear plant given the ignorance over the exact damage caused by either one.
Posted by: Benjamin Arthur Schwab at April 25, 2011 09:51 AMThe thing about coal, NG, solar and wind is when yer done just shut it down and walk away. With nukes, not so much. As WE see in Japan and Chernobyl, JUST shutting it down is YEARS of expert and experienced effort AND there's NO walking away & until its buried it WILL follow YOU. With Hydro, if the dam bursts, just get to high ground and YOU'll most likely live to build another. BUT, as I posted above, WE're gonna find out for sure.
Posted by: Mike Meyer at April 25, 2011 12:09 PMHola,
Felicito, el pensamiento excelente
http://easyddl.cz.cc/
DingoDogg
@pmpm - Thanks for rolling all of those issues up in one place. I've been thinking about many of them since you raised them, so this is a nice opportunity to address them.
1) The piece of "Not A Super Model" you don't like doesn't say exactly what you claim it does, in my opinion. I feel the statement from the BEIR VII report refers to effects at the cellular level - not at the level of an entire organism. I agree that higher levels of radiation correlate to greater levels of adverse health effects for entire organisms, and I've never said anything different. (Although I think there might be something to radiation hormesis for low levels of gamma rays.)
At the level of cells, though, I maintain that radiation effects which are adverse for cells can be beneficial for whole organisms. I have a research paper out of Hungary about lung cancer which supports this view but, look - it's simpler than that. If it weren't true, would there be any such thing as radiation therapy for cancer?
2) About the graph correlating worldwide production of nuclear energy to cancer rates in the US, I think you object to moving the graphs around, re-scaling them, and then overlapping them. I get why one might think that's fishy, but it's very legitimate. I swear up and down on my honor as a former math teacher that you're allowed to do it.
I agree with your point about latency rates and, after puzzling over it for several days, I don't think there's anything much to the graph. I still intend to track it out year-by-year to see if there really is anything there, but I haven't done it so far. If there really is a decline in cancer rates starting around 1995, I think it probably correlates to the end of atmospheric weapons testing. Which is an alarming statement about the effects of "background radiation" itself, if true, and also something I'm interested in investigating.
I took away something interesting from that post, however: the idea that maybe we should be looking at logarithmic rather than linear dose relationships. Because I'm dumb, this had literally never occurred to me before. But when I Googled around, I discovered that biology is full of examples of log-linear relationships. This was very interesting to learn, and I wouldn't have learned it without playing around. I hope other people who read Tiny Revolution view the site as a learning experience, too. I've certainly learned a tremendous amount from Jon.
About "incidence" versus "mortality", I don't get paid for this. Can't you cut me a break?
3) Your point about mathematics vs. physics is legitimate, as far as it goes, but I learned about this stuff in Physics 430 - Statistical Mechanics. What's more, when I do the math out, I find that the dose probabilities stack up to make a partition function, creating a conceptual framework similar to the Boltzmann derivation of the entropy expression S=k ln Omega. This is physics. So what?
The recent posts actually refer to a model in which the body is broken into 70 million separate interaction volumes. It examines decay probabilities in each of those small volumes, looking for large excursions. I think this is biologically reasonable; you are free to make your own opinion. My conclusion, which I hope I expressed clearly, is that most interaction volumes will experience at least one big BLAM! in a year as a result of an average decay rate which is very low. Raising the average decay rate appears to make the BLAM! bigger logarithmically rather than linearly.
I think that's interesting.
About forming a risk assessment, I agree that's the important part. And I'm getting there. But if I just up and spit it out, why would you believe it? Would you believe it if I wrote "Aaron M. Datesman, Ph.D." at the end?
You shouldn't.
Appreciate the readership and the comments. Sorry there aren't enough hours in the day to respond to many of them.
Posted by: Aaron Datesman at April 26, 2011 11:51 AM


