• • •
"Mike and Jon, Jon and Mike—I've known them both for years, and, clearly, one of them is very funny. As for the other: truly one of the great hangers-on of our time."—Steve Bodow, head writer, The Daily Show
•
"Who can really judge what's funny? If humor is a subjective medium, then can there be something that is really and truly hilarious? Me. This book."—Daniel Handler, author, Adverbs, and personal representative of Lemony Snicket
•
"The good news: I thought Our Kampf was consistently hilarious. The bad news: I’m the guy who wrote Monkeybone."—Sam Hamm, screenwriter, Batman, Batman Returns, and Homecoming
April 02, 2013
Sure, This One Goes To 11; But Can You Turn It Down To 0.11?
By: Aaron Datesman
I've previously written that our regulatory standards for exposure to low doses of ionizing radiation are based upon extrapolations downward from high doses. The framework is called the "linear dose model". You could say that I'm not fond of it. Perhaps my fundamental complaint (among the very many there are to choose from) is that the regulatory and scientific advisory bodies that utilize this model seem willfully blind to the idea that a "model" is a guess, rather than a law.
Since the linear dose model in reality is a guess, for its predictions to be credible it is absolutely necessary continually to audit the model to verify its accuracy. In the world we inhabit, unfortunately, this does not ordinarily happen. Instead, government and industry point to the predictions of the linear dose model to argue against any possibility of harm, forestalling meaningful audits of the model's validity. The circularity of the logic is perfect.
Nevertheless, the 1979 disaster at Three Mile Island was severe enough that a meaningful audit (albeit incomplete and not comprehensive) was actually performed. The data uncovered by that audit demonstrate convincingly that, for at least one type of exposure to ionizing radiation and one deleterious health outcome, the linear dose model is incontrovertibly incorrect.
In 1997, Steve Wing at the University of North Carolina - Chapel Hill published a reanalysis of health effects due to the Three Mile Island nuclear disaster, covering just the population in a ten-mile radius around the plant through the year 1985. The article, "A Reevaluation of Cancer Incidence Near the Three Mile Island Nuclear Plant: The Collision of Evidence and Assumptions", appeared in Environmental Health Perspectives - a peer-reviewed, open-access journal supported by the National Institutes of Health. The table below is lifted from his paper:
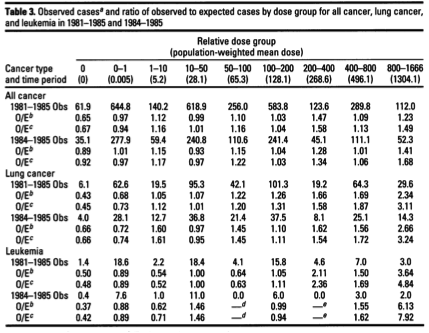
"O/E" indicates the ratio of Observed to Expected incidence of (not mortality from) cancer. If the doses were small and the exposures generally "safe", then one would expect to see values of O/E near one and no clear trend of increasing incidence with dose. This is sort of the story I see for "All cancer", the first section in the table* - at least, there's no clear dose response. It is important to point out, however, that this study ends in 1985. Since most forms of cancer have a longer latency than six years after exposure, this null result indicates only that the study didn't run long enough to demonstrate or rule out harm in this category.
The leukemia data is more substantive, but the truly interesting information relates to lung cancer, in which a clear dose relationship is evident. Joe Mangano of the Radiation and Public Health Project pointed this out in a letter to Environmental Health Perspectives; I wrote about it here.
Mangano ascribes the non-linear dose relationship to the "Petkau Effect", and claims that the mathematical relationship is logarithmic. The Petkau effect is a real (and very interesting) phenomenon in radiation biology, and I'm sympathetic to the idea that the dose response could be logarithmic in some situations. However, I'm unsure how the two concepts fit together. (Perhaps that information is contained in the original article by Petkau, which I have been unable to locate.)
In any event, the idea that the dose response might be logarithmic resonated for me. I thought about it a lot, and wrote quite a bit about it in April 2011, starting about here. For one thing, the idea that effects at high doses can be linearly extrapolated down to low doses is clearly nonsense. The linear extrapolation violates a basic teaching from statistical mechanics: the variance of a statistical quantity increases as its numerical value decreases. It irks me that the radiation health physics community apparently is exempt from this basic understanding, while I was required to grasp this idea in order to pass Physics 430 when I was twenty years old.
I set about learning what statistical mechanics might have to say about the possibility of a logarithmic dose response, and began to uncover relationships that seem to replicate the relationship that Mangano posited (posted here, for instance). But after a time I understood that I had approached the problem inelegantly (this is physics-speak for, "I wuz dumb,") and had conflated two separate phenomena in my head. The increasing variance in the decay rate is one; the other one is shot noise.**
The theory of shot noise was fully worked out by Walter Schottky around 1920. Schottky developed this theory to describe the operation of vacuum tubes. It turns out not to be possible to turn a tube amplifier down from "LOUD" to "quiet" (a linear extrapolation of volume downward) because electrons come in discrete packets that cannot be divided. Shot noise creeps in to destroy the performance of the amplifier on its most quiet settings.
Radioactive decays likewise come in discrete packets that cannot be divided. On this fundamental basis alone, the linear dose model cannot be correct. For instance, it's absolutely meaningless to consider the biological effect of 0.11 decays of an atom of radiostrontium adhered to your femur bone. But the linear dose model utilizes precisely this sort of understanding.
Many professors of electrical engineering, physics, or astronomy can, no doubt for a generous consulting fee, write down Schottky's equation from memory and then carry on with their business after shooing you away. This is the result*** for the average decay power (including the shot noise contribution) generated by a dilute system of radioactive particles. The total derivation in my notes takes up about seven lines and only barely requires calculus:
![]()
Among other situations, this equation would apply to a lungful of radioactive krypton or xenon gas expelled from the damaged reactor at Three Mile Island in Middletown, Pennsylvania, in 1979. The expression is fit**** to Wing's TMI lung cancer data in the graph below.
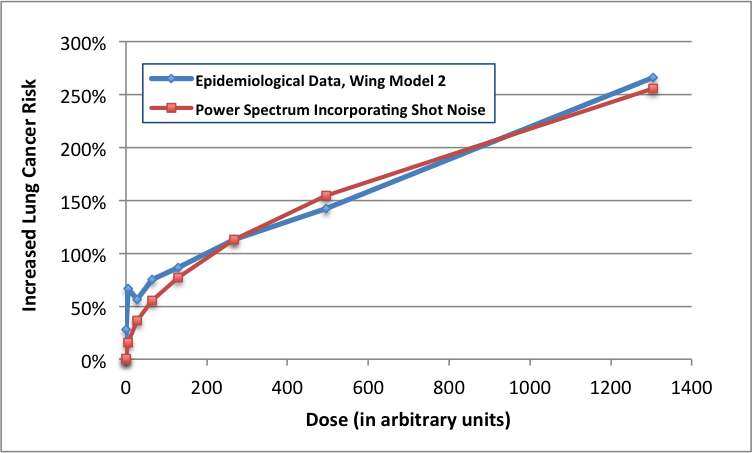
While it is impossible to prove a rule no matter how many supporting examples you acquire, all that's required to disprove a rule is one contrary example. The graph above - the result of an immoral experiment performed on innocent American citizens in March, 1979 - is the strongest possible counter-example to the linear dose model.
I don't believe the linear dose model, or any of the assessments of safety based upon it, because it's self-evidently contrary to the basic laws of physics and to the best available epidemiological evidence. The dial for radioactive decays and exposure goes up to 11, and even to 111 and beyond. But it doesn't have a setting smaller than one. Since this is true, the linear dose model cannot be correct - and it demonstrably is not.
So, understand this: when someone with authority explains that radiation is not very harmful and that only a very few people will suffer from the Fukushima disaster (or did suffer from Chernobyl, or TMI, or even from routine emissions generated by operating nuclear power plants), their judgment rests upon a thin veneer of science covering a steaming pile of horseshit. The scientific community has known the correct theory describing the shot noise power spectrum for nearly a century. That this knowledge has so far failed to penetrate the radiation health physics community is an astonishing scandal.
— Aaron Datesman
*Actually, in the higher-dose cohorts the cancer incidence seems to be 20% - 50% above the average, which is quite significant. But there's a wrinkle involving how the data are presented, so it's actually worse than that. For some reason, Wing chose to compare the cancer incidence in individual dose groups to the average incidence among the exposed population. (This is how O/E ratios below one at zero dose are obtained.) Perhaps this is standard in epidemiology - I have no idea - but if I had written the paper I would have compared the incidence in an individual dose group to the incidence in the group with zero dose. That comparison reveals an increase of cancer incidence in the high-dose group greater than 100% - that is, more than double.
** I imagine that these are related, actually. But that's a very mathematical tangent to the overall story that isn't very important.
*** Technical note: P is the instantaneous power dissipated through radioactive decay; this quantity is directly related to the density of free radicals generated by ionization events in the interaction volume, and thereby to the local chemical perturbation and to the health effect. E is the energy deposited in the interaction volume by a single decay, N is the average rate of decay within a single interaction volume, and Δf is the bandwidth of the biological response. This bandwidth is the inverse of the time required for the biological volume to return to its chemical equilibrium, which is on the order of 5 milliseconds. [1] There is experimental evidence supporting an interaction volume of approximately 1 cubic millimeter in size. [2]
Note also that the expression collapses to the linear dose model for large decay rates. When the decay rate in an individual interaction volume is small, however, the chemical response follows a square-root dependence. This shot noise contribution is much (for very dilute contamination, hundreds or even thousands of times) larger than the linear dose model predicts.
[1] Spitz et al., "Metabolic oxidation/reduction reactions and cellular responses to ionizing radiation: A unifying concept in stress response biology," Cancer and Metastasis Reviews, vol. 23, pp. 311-22, 2004.
[2] Belyakov et al., "Biological effects in unirradiated human tissue induced by radiation damage up to 1 mm away," Proceedings of the National Academy of Sciences, vol. 102, no. 40, pp. 14203-8.
**** This is a good fit; I made no effort to find the optimal fit, since the shape of the curve is the principal takeaway. (If it's a curve, then the linear model isn't valid.) However, the theory doesn't quite fit the very steep rise at very low doses. The divergence could simply reflect uncertainty and the effects of averaging within a dose group. It could also arise because the actual doses on the low end were higher than estimated. This seems plausible because the lowest doses would be the most difficult to estimate accurately.
As an added wrinkle, though, the little dip in the curve makes me wonder whether this is an example of the "biphasic" (or non-monotonic) dose response investigated by Professor Elena Burlakova of the Russian Academy of Sciences. That is too large a conjecture to hang on a single data point, however.
Wait a minute. If the relationship is more correctly: Cancer Incidence = log[ Dose ], then a linear model extrapolating down from high doses would err on the safe side for low doses. That is, it would overestimate the risk from low doses, rather than underestimate it. What am I missing?
Posted by: Cloud at April 2, 2013 09:53 PMI mean, if you fit a line to the last two data points (the ones around 500 and 1300 arbitrary units), clearly that line is greater than the red curve everywhere to the left.
So I'm not understanding the following: "When the decay rate in an individual interaction volume is small, however, the chemical response follows a square-root dependence. This shot noise contribution is much ... larger than the linear dose model predicts."
Posted by: Cloud at April 2, 2013 10:00 PM@Cloud, well, it's sqrt(dose), not log(dose) - I was incorrect about that. But the two functions are pretty similar over a portion of their domains.
The piece you're missing (I think) is that the shot noise model examines how many decays occur in a biologically relevant, small volume of 1 mm^3. This number is much, much less than one - say, 10^-8 per second, or something. The dose numbers on the x-axis refer to Wing's data, not the shot noise model.
The square root of N in this case is 10^-4, which is 10,000x larger. So the linear dose model is incorrect by a very large factor in this case.
Posted by: Aaron Datesman at April 2, 2013 10:00 PM@Cloud, oh, I see what you mean.
So, all right: suppose you're sitting at D=1000, and you're able to perform an experiment which administers an addition dose of 50 units. The risk of cancer incidence, according to the graph, increases by 7% or something.
If you're sitting at D=0, however, that increment of 50 units of dose increases the risk of cancer by 50%. The harm increases very rapidly at the outset.
Posted by: Aaron Datesman at April 2, 2013 10:12 PMOh, I'm sorry, @Cloud, I should go to bed. Ignore these comments.
The line you're asking about doesn't exist. Draw a line on the chart yourself, beginning at zero and extending to the right at a very, very shallow slope (possibly indistinguishable from the x-axis). That line represents the linear dose model. The shot noise curve and the Wing data are always far above that line, until they converge for N>>delta-f.
Posted by: Aaron Datesman at April 2, 2013 10:32 PMI had the same question as Cloud. From your last answer, I think the issue is, what exactly is the linear model? It seems you're saying that the linear model is drawn from some high-dose datapoint to the origin (since zero dose should have zero effect), is this correct? Whereas Cloud and I were both assuming that a linear model would be fit to several of the high-dose points, which would produce a line that intersects the y-axis well above the origin. If the linear model connects one high-dose point and the origin, then it greatly underestimates low-dose effects, as you're saying. Making clear what the linear model is would make your point more clear. Thanks.
Posted by: Ken M at April 2, 2013 11:39 PMI had the same question as Cloud. From your last answer, I think the issue is, what exactly is the linear model? It seems you're saying that the linear model is drawn from some high-dose datapoint to the origin (since zero dose should have zero effect), is this correct? Whereas Cloud and I were both assuming that a linear model would be fit to several of the high-dose points, which would produce a line that intersects the y-axis well above the origin. If the linear model connects one high-dose point and the origin, then it greatly underestimates low-dose effects, as you're saying. Making clear what the linear model is would make your point more clear. Thanks.
Posted by: Ken M at April 2, 2013 11:39 PMone other question: it appears what you are calculating for P is
E (Delta f) \sqrt{}
where C is the number of decays in a time period 1/(Delta f), \sqrt{x} means squareroot of x, and is the average of x. Why is \sqrt{} the right quantity to use to calculate average power, rather than ? Thanks.
Posted by: Ken M at April 3, 2013 12:17 AMhmmm ... I was using angle brackets for average, and it appears they get edited out of your commenting system. Let me try again.
it appears what you are calculating for P is
E (Delta f) \sqrt{ [ C^2 ] }
where C is the number of decays in a time period 1/(Delta f), \sqrt{x} means squareroot of x, and [ x ] is the average of x. Why is \sqrt{[ C^2 ]} the right quantity to use to calculate average power, rather than [ C ]? Thanks.
Posted by: Ken M at April 3, 2013 12:19 AMI would like to add a few excerpts from What's New. It is a blog by Robert Park, a professor of physics at University of Maryland. Link is http://bobpark.physics.umd.edu/index.html
1. DOES EXPOSURE TO LOW-LEVEL GAMMA RADIATION INCREASE LONGEVITY? (Friday, 13 December 1991 Washington, DC)
Well, it seems to for workers in nuclear shipyards. The final report of a ten-year study to determine whether exposure to low-level gamma radiation is associated with an excess risk of cancer has been released after being held up for three years. Perhaps the best epidemiological study ever done of exposure to low-level occupational radiation, it compared workers in non-nuclear ship-yards to workers in nuclear yards who were exposed to radiation. The surprising finding was that nuclear workers had significantly lower mortality rates from all causes than their non-nuclear counterparts--and those with the greatest exposure had the lowest rates. No one seems ready to suggest that low-level radiation is good for you. But, in a review of the report, John Cameron of the University of Wisconsin, a physicist who served on the Technical Advisory Panel for the DOE study, points out that if the study had found an excess of 24% in mortality among nuclear workers, instead of a 24% deficit, the report would have been on CBS News.
1. NUCLEAR RADIATION: BEYOND THE LINEAR-NO-THRESHOLD MODEL. (Friday, April 15, 2011)
On Tuesday Japan raised the severity rating of the Fukushima nuclear crisis to 7, putting it on a par with the 1986 Chernobyl disaster. Although Japan is releasing few details, you can safely conclude that radiation is really bad; beyond that you're on your own. The most up-to-date and comprehensive risk estimates for cancer and other health effects from exposure to low- level ionizing radiation are in the 2006 Biologic Effect of Ionizing Radiation Report of the National Academies (BEIR VII). The only data base we have is from victims of massive exposures at Hiroshima and Chernobyl. The report relies on the linear-no-threshold model to estimate the risk from multiple exposures at much lower levels, such as airliner crews. This is not only wrong, they know it's wrong. A DNA repair process is constantly at work in human cells repairing DNA damage from sources of ionizing radiation, including UV light and cosmic radiation. There is not much choice but to ignore the repair process and assume a linear model which greatly overstates the risk from multiple exposures. A panel of experts concluded that that, "the preponderance of evidence indicates that there will be some risk even at low doses."
2. HORMESIS: THE LINEAR NO-THRESHOLD MODEL MUST BE WRONG. (Friday, March 18, 2011)
Airline crews experience a high total-radiation exposure. But the exposure of airline crews is spread over many years, while Chernobyl survivors got a concentrated dose. Statistically they are not distinguished. Do the derivatives matter? According to a story in the news this week, Chernobyl survivors today suffer cancer at about the same rate as others their age. The same is true of Hiroshima survivors. If true, it would seem to support the radiation-hormesis thesis. "Hormesis" refers to things that are toxic in large doses, but harmless or even beneficial in small doses. Trace amounts of selenium, for example, are essential for cell function of animals. But selenium salts in larger doses, are highly toxic. Airline pilots or not, we are all exposed to background levels of ionizing radiation every day of our lives. We do not all succumb to cancer. It seems there is a repair mechanism that compares neighboring strands of DNA and patches up damage. The comparison can work only if damaged strands are isolated. If the damage rate is very high, the same repair mechanism could multiply the damage.
@Ken M, the equation for power derives almost immediately from the Schottky equation for shot noise, which you can look up. It's only necessary to substitute the energy E in a decay for the charge q, which is quantized in a current.
I agree that I should have put a line for the linear dose model in the figure. Maybe I'll make that change.
Posted by: Aaron Datesman at April 3, 2013 04:55 AMThis line
if the study had found an excess of 24% in mortality among nuclear workers, instead of a 24% deficit, the report would have been on CBS News.
tells me everything I need to know about Robert Park. He probably also thinks that Walter Cronkite lost the Vietnam War for the US, and that Dan Rather's report on Cesar Chavez and farm worker exploitation was paving the way for a Soviet takeover. He and my dad would get on just fine.
Posted by: NomadUK at April 3, 2013 04:56 AMAaron, like Cloud and Ken I don’t quite get your shot-noise curve. If it collapses to Linear non-Threshold at high doses, but then curves sharply downwards at low doses as you’ve drawn it, it seems that LNT would overstate risks at low doses. And I don’t see how it could converge with LNT if the actual LNT line is, as you suggest, very shallow and almost indistinguishable from the X axis.
In fact the shape of your curve looks like what the sub-linear threshold alternative to LNT proposes, but shifted a bit—linear at high doses, but then curving downward at low doses to cross the x-axis at a threshold radiation dose above zero. It may or may not be true, but at least it’s consistent with a high-dose LNT curve that goes to zero at zero radiation. But it also implies that LNT overpredicts radiation risks.
I don’t know if it’s appropriate to hang everything on the Wing paper, which is not too representative of the literature. Other studies, like this (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1241392/pdf/ehp0111-000341.pdf) and this (http://www.ncbi.nlm.nih.gov/pubmed/21855866) show no consistent effect of TMI radiation exposures on cancer incidence and mortality, or other mortality, and they cover much longer time periods than the 6 years covered in the Wing study. In the epidemiological literature as a whole, it’s a statistical toss-up whether there were small cancer effects from TMI, or none at all. The notion that TMI radiation caused catastrophic public health effects is not too defensible.
That’s true for the rest of radiation epidemiology. The scientific debate over low-dose radiation risks is not “huge versus small” but “small versus none.” And that follows not from theoretical dose-rate models but from the blunt empirical finding that when you count up the cancer and other health effects resulting from low radiation doses, they turn out to be modest to nil.
I don’t understand your shot-noise theory. As near as I can make out, you’re claiming that at low doses individual alpha, beta and gamma particles can do much more damage to a cell than they can at higher doses. I can’t see why that should be true. A higher dose simply means that there are more particles hitting cells and causing free-radicals that can damage DNA, so there is a greater chance that somewhere in the body one of them will trigger a cancerous mutation. Or a higher dose might overwhelm DNA repair mechanisms; that’s a biphasic model that means radiation risks will soar after a threshold. But again, that would imply that LNT overpredicts rather than underpredicts radiation risks at low doses.
What am I missing?
Basically, that power equation is finding the instantaneous power 1 sigma above the average power--roughly,the height of the spikes. It boils down to saying that when the decay rate drops below one event per 5 milliseconds (or whatever time unit you think biologically significant), you're going to see nothing, nothing, nothing, spike, nothing, nothing, spike, etc... The majority of the spikes will be single decay events.
I had more to add along the lines of what Will wrote--the linear hypothesis is that cancer risks are proportional to the number of particles absorbed. You get a quadratic term if you think that cells are much more likely to become cancerous if two particles hit in quick succession. The whole idea of shot noise or Poisson statistics underlies the linear/quadratic model as best I can tell.
I haven't looked back at the previous threadc--maybe you dealt with this there. No time to look right now.
Posted by: Donald Johnson at April 3, 2013 09:49 AM1) Linear is different then affine. A linear equation must pass through the origin and thus a linear model would take a data point at a large dose and assume that the danger at zero dose is zero and draw a line. An affine equation is a linear equation with an affine offset (linear think y=mx and affine think y=mx+b). An affine model would as suggested above would overstate the risk at low doses but a linear model, as Mr. Datesman points out, would underestimate the risk at low doses. In my undergraduate physics education I learned the importance of differentiating a linear model from an affine model and something of when and how to chose the correct model. The data in the paper by Dr. Wing does support that the linear model is incorrect but I also know that one or a small number of studies isn't that important and I don't know how many good studies of the linear dose model have been done.
2) Even if the question isn't large vs. small but rather small vs. none then that appears to still be a very important question and relatively speaking small is more greater to none then large is greater to small. Even if there haven't been catastrophic health effects from some radiation release (from a societal perspective) that doesn't mean that the health effects don't exist at all and that one person dying from an incident like at Three Mile Island had a health effect that is catastrophic to that person's family.
3) There appears to be two different questions that I think are the same but I'm not sure. There is the question of "How worried should an individual be about low exposure to radiation?" and a public health question of "How many more cancers will there be in society due to small releases of radiation?" If I understand your argument, Mr. Datesman, then the individual should be more worried about exposure to low radiation doses then they are currently being told to worry and that this would also mean that there will be more cancers in the US due to releases of low dose radiation that is currently being claimed. I think that this also means that there should be more cancers in a society that has more exposures to low levels of nuclear radiation then another society that has the same total amount of radiation exposure but in larger doses if a log or square root no threshold model is correct. I'm not sure on my claims here. Please correct me if I'm wrong.
4) There also seams to be an underlying question of is nuclear radiation exposure good or bad or neutral, which I don't think is a productive question. I think that industries that release nuclear radiation and other carcinogens often provide benefit both to individuals and to society but also provide the costs of increased cancer rates which harms both individuals and society. My response is to tax these industries and use part or all of that money to pay for cancer treatments. Figuring out how much to tax each industry is a difficult and important task and what model for radiation exposure danger to use is an important question in answering the first.
5) There is also the question of how to we treat individuals who have have gotten ill due to low doses of radiation regardless of exactly how high that individual risk is. I hope that nobody here is suggestion that, for example, because the risk is small that someone who becomes ill because of an incident like at Three Mile Island doesn't deserve assistance and compensation paid for by the company owning or operating Three Mile Island, the nuclear industry, and/or from government.
Posted by: Benjamin Arthur Schwab at April 3, 2013 01:35 PMWhat's missing?---ANY&ALL documented data on cancer death causes from BEFORE July 1945.
Posted by: Mike Meyer at April 3, 2013 02:38 PMWith all due respect, I don't think your analysis makes a lot of sense.
First, there's no reason to think that power should be proportional to increased cancer lung risk, so there's no reason to think that the Schottky's equation should fit Wing' TMI lung cancer data. It's true that there's no clear evidence that increased cancer risk should be proportional to radiation dosage at low dosages, but you're just substituting the linear dose model with a different arbitrary linear relationship. (And an arbitrary linear relationship that doesn't appear to make a of theoretical sense.)
Second, you appear to be misinterpreting Wing's TMI lung cancer data. If the blue empirical line in your graph were accurate, there would be no reason to talk about Schottky's equation, or perform any theoretical analysis, because the blue empirical line claims that even for people with very tiny dosages, the risk of lung cancer is increased 30-70% relative to people with no dose. If this were true, it would be clear that the linear model was incorrect. However, this is not what Wing's paper shows. The ratio of observed to expected cases in their table 3 defines the denominator of "expected cases" as the number of cases expected for the population around TMI as a whole. So, for example, a value of 0.68 for low doses means that people in low dose regions around TMI were 68% as likely to get cancer (32% less likely to get cancer) than people around TMI generally. It doesn't mean that people in low dose regions were more likely to get cancer than if the TMI accident never occurred.
Third, the linear dose model does not claim some weird understanding of the biological effects of 0.11 decays of an atom. For any dosage that we're ever going to think might have some noticeable effect, the number of decay interactions will be some very large integer, and it won't be relevant if it's 3,678,156 decays or 3,678,157 decays. It's true the linear model wouldn't make sense when you get down to the order of 1 radiation interaction, but no one in their right mind would claim that it did, you're attacking a straw man, and a fairly insane straw man at that. The linear model is questionable because it's not clear how the body will respond to those decay interactions, but it's not questionable because scientists are so stupid as to think that there can be 0.11 decays of an atom.
Posted by: Winter Wallaby at April 3, 2013 07:02 PMYeah, following up on the wallaby's remarks, I can't see why the statistical fluctuations in the instantaneous power would matter. When you get down to the point where the fluctuations are large compared to the average, you're also down to the point where you're talking about multiple numbers of your 5 ms time intervals where there is no decay, punctuated by occasional intervals when a decay occurs. (That's what I meant by the nothing,nothing spike comment above). Why would that show that low dose rates are disproportionately more harmful than large dose rates?
Also, fleshing out another of wallaby's comments, a whole body dose of 1 millirad means 0.1 erg per gram. That's 6 x 10 ^ 11 eV or assuming 1 MeV radiation for the sake of round numbers, 600,000 gamma rays or beta particles or alpha particles per gram. A 100 kg person (round numbers again) would be absorbing 6 x 10^10 particles over his or her whole body.
Your "interaction volume" of 1 cubic millimeter would be about 1 milligram, so that's equal to the energy of 600 gamma rays or beta particles or whatever, for a dosage of 1 millirem. (It would actually require many more gamma rays, since they won't be stopped in a distance of 1mm, so each one deposits a small fraction of its energy in your interaction volumes and many more than 600 pass through to give a dose of 1 millirem.) So if someone says the dosage is 1 millirem or higher for a given volume, aren't we already outside the range where statistical fluctuations matter that much?
Posted by: Donald Johnson at April 3, 2013 07:51 PM"Why would that show that low dose rates are disproportionately more harmful than large dose rates?"
That's poorly worded. The following probably won't improve it much, but I meant, why would the fact that dose rates of less than 1 decay per 5 ms show much larger percentage variation of decays per 5 ms compared to dose rates much higher than 1 decay per 5 ms somehow demonstrate the low dose rates inflict much more harm than the linear no threshold hypothesis suggests? (Okay, that probably was worse than before.)
If anything, the relevance of the Poisson distribution is that you get many fewer cases of 2 or more particles hitting a given cell in a given time at low dose rates than at high ones. For the 2 particle case, it's proportional to the dose rate squared, so low dose rates are less dangerous than a purely linear model suggests, if it turns out that cells could repair the damage from 1 hit, but would be overwhelmed by 2 in quick succession.
Posted by: Donald Johnson at April 3, 2013 08:02 PMTwo more posts and I'll shut up for now.
Googling Steve Wing, it doesn't appear he has any problem with the linear no threshold hypothesis. His claim about TMI is not that low doses caused cancer increases, but that the doses were much higher than claimed and those caused cancer increases. In the link below he says there were reports of vomiting, hair loss, etc.., which if true sounds like radiation sickness, implying very high doses.
Posted by: Donald Johnson at April 3, 2013 08:16 PMThe post below shows Stephen Wing explicitly using the linear no threshold model--
Posted by: Donald Johnson at April 3, 2013 08:17 PMA quick response, but I'm tired.
Wing does say that the doses were high, and I think he's right. It's certainly correct that we don't know that the doses weren't high. But in a graph that goes all the way to zero, some of the doses were low. In fact, it seems from the fit parameters that the doses were low enough that the shot noise contribution dominates.
Also, I know that Wing applies the linear dose no threshold model. I read his paper. This doesn't mean he's correct. As far as I know, what I've written here is entirely a new thing. It's also obvious to anyone with my background in astronomical detectors. And if you think it isn't correct, then kindly explain why the fit to the data is so good.
Look, this is basically how it works.
Take the example where the average decay rate *in the interaction volume* is 0.02/sec. (Refer to the paper by Belyakov to understand why the 1 mm^3 volume is appropriate. I could go on on this topic, but I refrain.)
There's a chalkboard, and it's erased every five milliseconds. This corresponds to a frequency bandwidth for noise power of 200 Hz. Whenever there's a decay in the interaction volume, make a mark on the chalkboard.
The population around TMI was exposed for around three days. (At least, this was the duration for which Xe-133 was recorded in Albany, NY.) So, work this out: what's the maximum number of marks you're likely to see on the chalkboard?
The answer is FOUR or maybe FIVE, a factor of 250 larger than the average rate of 0.02 disintegrations per second. I'm sure you can do the math verifying this.
Now, consider: every disintegration dissipates about ~500,000 eV of energy in the volume. Each ionization event eats up about 50 eV of that. That's 10,000 free radicals per disintegration, in that small volume, for a very short time.
Why anyone would think an average value WHICH CAN'T EVEN EXIST BECAUSE A SINGLE DECAY CANNOT BE SUBDIVIDED represents the health effect of this excursion from chemical equilibrium eludes me totally.
Last point - what I wrote is not sufficiently explicit, but it applies only to internal contamination from alpha- and beta- emitters. The path length of gamma rays in tissue is ~10cm or so, which exceeds the scale of the interaction volume substantially. I'm reasonably willing to accept a linear dose model for gamma and X-rays.
Posted by: Aaron Datesman at April 3, 2013 10:34 PMSince you have several free parameters, and only about five data points over an appreciable range (i.e. when you exclude the few clustered around zero), that's not a particularly good fit. And since, as I already pointed out, Wing's paper does not in fact have data in it that produces the blue curve, and the blue data points are only based on your misunderstanding of his table 3, any goodness of the fit is particularly spurious.
If the curve you had drawn in blue was actual correct empirical data it would be completely obvious that the linear model was wrong. No theoretical analysis or fitting is needed to notice that the blue data points are quite far from a line passing through the origin. If so, for Wing to fail to make this very simple observation indicates that he's such an extraordinary moron that it's rather surprising that he was able to spell all the words correctly in his paper title, let alone correctly perform the adjustments for socieconomic data described in his paper. So you need to decide between two possibilities: (1) Wing, and everyone else working in his field, are all such extraordinary morons that they've failed to notice that they have good data for the last 16 years that, with a two second glance, obviously demolishes the linear model or (2) you've misunderstood his table 3. I'd like to point you to this comic, and gently suggest that consider option 2 a little more seriously.
Posted by: Winter Wallaby at April 4, 2013 12:20 AM@ Donald Johnson,
--I agree with you; even at low doses, there’s enough residual bombardment with particles that the increment should have linear effects.
That’s especially true if you take account of background radiation, which is 2.4 msv per year external and internal. There’s no such thing as a pristine radiation-free baseline where a tiny increment of radiation can have non-linear Poisson effects. (Which I don’t even understand.) Even at zero TMI dose, subjects are still being bombarded by hefty amounts of background radiation, so the modest TMI increment must surely have come in a *total* dose range which is far above where spiky statistics are important.
--We really must view Wing’s anecdotal evidence about nausea, hair loss and pet die-offs with extreme skepticism. Remember, in any population of hundreds of thousands of people, as around TMI, there will be at any given time a fair number of people with upset stomach, people who are losing hair (I am right now, alas), and pets that die. Unless we can establish a baseline incidence of those effects in the absence of TMI radiation, the anecdotes are meaningless. We also have to factor in the possibility that the fear of TMI made people exaggerate or mistime their recollections of maladies and pet deaths to fit their anxieties about radiation risk.
Symptoms of accute radiation sickness like nausea and hair loss and animals dying in their tracks do not show up until doses are in the thousands of millisieverts. No symptoms like that have been reported at Fukushima, a much vaster spew than TMI, even among emergency workers at the plant. It’s extremely hard to believe, then, that people around TMI could have received such high doses.
The consensus estimates are that the highest doses at TMI were around 1 to 2 mSv. To cause those accute symptoms the actual doses would have had to have been a thousand times greater than the estimates. But if radioactive plumes dense enough to deliver those Sievert-sized doses over a few days—hugely larger doses and dose-rates than anyone received from the Fukushima spew—had actually been drifting around, they would have been impossible to overlook.
So no, I’m not buying the anecdotes about hair loss and nausea and pet deaths. They just don’t add up.
@ Aaron,
I’m afraid I still don’t understand your shot-noise theory. Could you try to specificy exactly which physical and biological phenomena become proportionately more damaging at low as opposed to high doses, and why?
I’m not sure, but I think I see one way that you might be going wrong. You keep discussing the effects of radioactive decays at “interaction volumes” of a cubic millimeter or so. That’s fine, but it’s conceptually wrong, a category error, to apply that concept to macroscopic dose-response curves.
That’s because dose-response curves like LNT are not theoretical constructs derived from models of microscopic cellular damage. They are strictly empirical relationships, and they are defined, not extrapolated to but defined, on either a whole-body or a macroscopic organ basis.
Heres what I mean:
LNT is simply an empirical equation fit to a set of data points, and those data points are: how many cancers in a collection of whole organisms result from a certain exposure of radiation to the whole body. Sometimes dose- response curves are made for a single organ, especially thyroid glands, and there the data points are how much thyroid cancer results from a certain radiation exposure of the whole thyroid.
LNT is not, I repeat not, defined as the amount of radiation damage that occurs to a single cell hit by a gamma ray or a beta particle, or the damage that occurs from a single radioactive decay inside an “interaction volume.” It just is not defined that way; it is defined at a wholly different analytical level.
Because the definitional perspective is the whole body or macroscopic organ, not the cell or interaction volume, what matters in a macroscopic dose-response curve is the amount of radiation impinging on the whole body or organ. And from that perspective, the spiky statistics of rare decays in tiny interaction volumes don’t matter at all. From a macroscopic perspective, the one that defines LNT, whole bodies and organs are always awash in huge numbers of radioactive decays. Just counting the internal radiation from naturally occuring isotopes, every adult whole body experiences 7000 decays per second. A whole body doesn’t experience low-dose radiation as a rare shot-noise impact with a flukey power spectrum, it experiences it as an infinitesimal increment to an always huge number of decay events. And the dose-response mathematics of low-dose radiation from that macro perspective are continuous, smooth and linear.
So your complaint about scientists positing fractional radioactive decays is a profound misunderstaning. LNT is meant to represent collectivities for which radioactive decays are never less than tens of thousands per second. Your Poisson-ish shot-noise analysis, which I do not understand, is simply not applicable to the analytic framework of macroscopic dose responses.
Will is correct, NO baseline. (also no mention of particulate ingestion or gas inhalation, SURELY some chunks flew out of TMI)
Posted by: Mike Meyer at April 4, 2013 01:44 AMNO known threshold at where cancer begins, NO ACCURATE data collected at the event(certainly none published as the operators of TMI were bent on PR instead of public awareness, much like TEPCO), NO real picture of what cancer events look like without background radiation or at what point background radiation places a cancer patient toward THAT threshold. (ex: a sip of water to a drowning man)NO exhumations, NO autopsies, Mr. Wing has nothing but guesses.
Posted by: Mike Meyer at April 4, 2013 02:04 AMAaron, in your example the linear model would do this. Three days is about 250,000 seconds. At a decay rate of 0.02 per second, in those three days your interaction model would experience 5000 disintegrations. Multiply by the energy and the relative biological effectiveness and divide by the mass (about 1 milligram) and you'd have the dose. You're apparently calculating the maximum number of disintegrations you'd see in some 5 ms period. Maybe I'm making an arithmetic error (easy to do), but for four decays in your 5 ms, with an average decay rate of 0.02 per second, I don't expect to see 4 decays in any 5 ms time period in those three days. Did you mean 0.02 per 5 msec? I think you probably did. If so, multiply my 5000 by 200--there would be 1 million decays and that's the number that would be used to calculate the dose.
Posted by: Donald Johnson at April 4, 2013 12:20 PMI imagine that the radiation health community gets quite a few tidy little sums from the nuclear industry for research and such. As always the answer is its no worse than a couple of x-rays&the big chunks taste just like chicken.
Posted by: Mike Meyer at April 4, 2013 02:47 PMMike Meyer- Somehow I think you're the only one here who appreciate this, so addressing it to you...
Remember way back when Aaron was posting about the Holowka (sp?) farm outside Harrisburg, Pa WRT the TMI accident? Well, it sparked my interest do I went digging online for more info and to see just where their farm is on the USGS topo map to see of the heavy radioactive cloud theory passed the sniff test. Long story short, while lots of places cited the story of what happened, it seems no one knew where it was other than the rural deliver address, which was the closest town. I happened to be doing a bit of land title research in PA a while later and tracked it down, and by golly if the topography match the sort of funnel that would have channeled and held heavy gasses for a while. I live a couple hours from there, so offered to go dig serruptucious soil samples for Aaron to prove/disprove his theory, but sadly neither of us had funds to send samples off for the necessary testing.
Anyway, on a broader note, I think most folks here are missing the forest for the trees as they nitpick the minutea of the post. Quite clearly the story (told by his numerous posts on the subject) has to be taken as a whole. Short version is that "safe" levels were quite arbitrarily assigned, and when it comes to the effects of low levels of exposure "safe" is understating the effects be orders of magnitude. As Aaron mentioned, this is a new thing, and a direct application of an EE theory accepted as gospel for a century.
Posted by: Aric at April 4, 2013 04:00 PMMike Meyer- Somehow I think you're the only one here who appreciate this, so addressing it to you...
Remember way back when Aaron was posting about the Holowka (sp?) farm outside Harrisburg, Pa WRT the TMI accident? Well, it sparked my interest do I went digging online for more info and to see just where their farm is on the USGS topo map to see of the heavy radioactive cloud theory passed the sniff test. Long story short, while lots of places cited the story of what happened, it seems no one knew where it was other than the rural deliver address, which was the closest town. I happened to be doing a bit of land title research in PA a while later and tracked it down, and by golly if the topography match the sort of funnel that would have channeled and held heavy gasses for a while. I live a couple hours from there, so offered to go dig serruptucious soil samples for Aaron to prove/disprove his theory, but sadly neither of us had funds to send samples off for the necessary testing.
Anyway, on a broader note, I think most folks here are missing the forest for the trees as they nitpick the minutea of the post. Quite clearly the story (told by his numerous posts on the subject) has to be taken as a whole. Short version is that "safe" levels were quite arbitrarily assigned, and when it comes to the effects of low levels of exposure "safe" is understating the effects be orders of magnitude. As Aaron mentioned, this is a new thing, and a direct application of an EE theory accepted as gospel for a century.
Posted by: Aric at April 4, 2013 04:01 PM@Donald Johnson,
Take the volume of the lungs as 3 liters - that's 3 million interaction volumes. The number of interaction volumes times the number of time intervals (that's Nv * T) equals the number of trials.
The maximum number of decays you're likely to see in any one interaction volume is the number N for which the Poisson distribution gives a probability of about (NvT)^-1.
Your claim that you don't expect to see four decays in an interaction volume is not correct. For 0.02/sec and 5 ms, go ahead and work it out. You'll find that:
about 13 interaction volumes experience six decays simultaneous within the "reset time";
in 382,000 interaction volumes, there will be five decays (certainly some of them in the same biological volume, multiple times during duration of exposure);
980,000 instances of four decays;
196 million instances of three decays;
etc.
This is basic physics, and not open to dispute. It's only interesting because I've proposed that the decay rate must be measured to the biologically appropriate scales of time and volume. The mathematical structure to describe this was fully worked out nearly a century ago, as I noted.
Posted by: Aaron Datesman at April 4, 2013 04:09 PMI'd be interested to know the lat/lon of that farm myself to compare to maps of the known geographical features of that area. That, "blup, blup, blup, like water bubbling underground" bit got me thinking about the karst in the area. By my calcs, she would have been 7 to 9 miles from the reactor itself so it seems a bit far for the sound to travel - esp. with that description.
Posted by: Some Guy on the Innurnet at April 4, 2013 04:20 PMSome Guy- odd thing about PA deed searches is you pay by time logged in, not search time. So when what I was searching for finished much earlier than expected I spent the remainder of the time locating that farm. Wasn't that hard, IIRC, and really only took half an hour or do to track down a street address (Iirc farm passed to the daughter and then was sold off in the '80's, or something like that). Anyway, if you have a way to get samples tested, I'd be more than happy to take a drive...
Posted by: Aric at April 4, 2013 04:47 PMBtw, this is my issue with some of the folks above, who I may or may not be butting heads with in another thread. In the case of this post, it's accepted science and frankly I'm surprised at the reaction. In the case of first hand accounts of TMI locals, I'm surprised by the fact that no one has done the basic testing to prove whether exposure over the midatlantic was indeed greater than they said. While I can understand the political implications of a government mea culpa, that doesn't make it right, or justify continuing that course.
Posted by: Aric at April 4, 2013 05:11 PMAaron, I thought you meant one interaction volume, not all the volumes in the entire volume of the lung. So I'd have to rework the math--I'll do it later. I thought you might have meant 0.02 decays per 5 ms, because you said that finding 5 decays in 1 of those time periods was 250 times the average rate of 0.02 per second. But 5 decays in 0.005 seconds is equivalent to a momentary rate of 1000 decays per second, which is 50,000 times greater than 0.02 per second.
So if you mean 3 million interaction volumes, each with .02 decays per second, in 3 days that means 15 billion decays. Again, the linear hypothesis is that the risk is proportional to the total number of absorbed particles. So they'd take the 15 billion decays, multiply by the energy and divide by the mass of the lungs (or whatever it is we're looking at.)
Posted by: Donald Johnson at April 4, 2013 05:32 PM@Donald Johnson, I appreciate you telling me how dose is calculated, but I certainly know this - it's lifted directly from the physics describing ion implantation, about which I know a great deal.
So, if the linear hypothesis is correct, why is there not a line when I graph out Wing's data? I think it's because the proper physical relationship is between power and the chemical state of living tissue, not energy (the time integral of power) and biology.
Regarding 5 decays in 5 ms when the average rate is 0.02/s, I was incorrect. (While I was working out this understanding, I was accustomed to setting the frequency bandwidth =1. I haven't entirely adjusted my thinking since researching the chemical kinetics of free radicals in living tissue.) So the power is actually larger by a factor of 5/0.02/.005 = 50,000. Thank you for the correction.
But I believe it supports the point I've made.
Posted by: Aaron Datesman at April 4, 2013 06:10 PMAric: THANK YOU! But I think the math has to be done before WE can remotely understand what has happened& it looks like no one else making much of a stab at it here in the USA. Japan? I just imagine they're on top of it and probably the best resource for data concerning health effects of radiation.(perfect laboratory considering Hiroshima to Fukushima)
STILL, IMHO, without cancer data from before the nuclear age WE stay on a sliding scale and it becomes impossible to have an accurate picture.(also "shot noise" from PR campaigns by the energy corps. and their buddies in the Nuclear Regulatory Commission)
I might be misunderstanding something. I just want to get the numbers here.
3 days is about 2.5 x 10^ 5 seconds
Multiply by 200 (because of the 5 ms time) and you get 5 x 10^7
multiply by 3 million interaction volumes and you get 1.5 X 10^14 trials
Now at a decay rate of 0.02 decays per second in one interaction volume and a time period of 5 ms, that's an expected number of decays that equals 10^-4. Call that D.
Poisson distribution
Probability of n decays in 5 ms in one interaction volume = D ^ n times exp(-D) divided by n!
exp(-D) is very close to 1, so
prob (n) is about D^n / n! or 10^(-4n)/n!
Multiply this by 1.5 x 10^14 and you get the expected number of one decay events, two decay events, etc...
I find
1.5 x 10^ 10 one decay events (of course)
7.5 x 10^5 two decay events
25 three decay events
and that's it. Don't expect any 4 decay events.
I could be having a brain fart or misunderstanding what numbers I was supposed to use.
Fun fact--double the dose rate and you get twice the number of single decay events and quadruple the number of 2 decay events. Hence the linear/quadratic model.
Posted by: Donald Johnson at April 4, 2013 06:16 PMAaron, part of my point is that radiation biologists don't make this bizarre assumption that decaying atoms split into ten thousand pieces and decay one ten thousandth at a time. in your lung example there would be 15 billion hits, and that's what they would focus on, not this 0.02 decays per second per interaction volume you focus on. With my correction, you're dramatizing that when 1 to 5 decays do happen in a short time, the rate of energy delivery is temporarily 10,000 to 50,000 times higher than a statistical average value that never happens. So what. You actually think people didn't know that radiation is delivered in chunks? The linear dose hypothesis is based on the idea that a particle of a given type, the risk of cancer caused by radiation is directly proportional to the number of particles that are absorbed. Your focus on the shot noise effect would be relevant if it turns out that risks go up disproportionately if two or more particles hit a given cell within a given amount of time (perhaps this 5 ms you refer to). But Poisson statistics shows that the risk of this happening varies with the nth power of the dose for an n particle event. So it works against the idea that low dose rates would be more dangerous than people think.
If there's some real evidence of harm from low doses (I'll let others argue about that), far greater than the mainstream radiation health scientists acknowledge, fine. But I don't see how the shot noise argument justifies it.
Posted by: Donald Johnson at April 4, 2013 06:47 PM@Donald Johnson,
Thanks for the comments, they are useful.
First: your numbers for 3-decay, 2-decay, and 1-decay events are correct. I used D=0.02, again forgetting to scale for 5ms. (The Wing data is firmly within the shot noise limit, so the bandwidth is irrelevant. If this had not been the case, I probably would have failed to interpret the data in this way.) This is why I should stay away from comment threads, I never have the time to give them my full attention.
However, your statement:
"Fun fact--double the dose rate and you get twice the number of single decay events and quadruple the number of 2 decay events. Hence the linear/quadratic model."
is correct, but incomplete. If I double the dose rate, how quickly does the number of five-decay events arise? We both know the answer is around 32x for low doses. (Interesting that it's less than this for higher doses, right? That's because the variance goes up as the numerical value of a statistical quantity decreases.) And it's quicker for larger values of N.
The fact that the probability is finite for all values of N explains why it's necessary to examine the power spectrum (which is continuous), rather than a silly Taylor expansion like the linear-quadratic model. I think you have the background to understand this statement.
If I had written a post with full technical content, I would have addressed the complaint you raise. There is an implied causal chain in the linear dose model: energy -> chemical state -> health effect.
My point is that the chemical state perturbation is delivered very intermittently in chunks of 10,000 or more free radicals. This is very different than assuming a linear relationship between the dose and the chemical state. For instance, at 0.02 decays/sec and 500 keV/decay with a 200 Hz bandwidth, that's a perturbation of just 1 free radical.
Now, are you seriously telling me that these two situations are equivalent? Because here's what is really happening:
The linear dose model is telling me that someone is tickling my balls. In reality, most of the time nothing happens; but once in a while somebody troops up and kicks me in the nuts.
Bottom line.
Thank you for correcting my math errors, by the way. It's impolite of me to waste your time in that way. I started a new job at NASA, and probably should not have chosen to pick this up again just right now....
Posted by: Aaron Datesman at April 4, 2013 08:05 PMDon't worry about the math errors. I made a few offline yesterday just calculating the number of decay events in one of your interaction volumes(not realizing you were talking about the whole lung)--I forgot to multiply by the 200, for one, and I forget what the other one was. I think I finally got it on the third or fourth attempt.
But I'm baffled by the way you think the mainstream view assumes that the energy is deposited in some gentle gradual fashion over the target volume. I mean, it's IONIZING radiation--that's the point. 500 Joules of gamma rays will kill you, but 500 Joules of visible light photons is about one second of sunshine if you sunbathe, a nice feeling on the skin and if distributed evenly throughout your body it'd warm you by some tiny fraction of a degree. (Too tired to do the trivial math.) Your emphasis on how getting one or more decay events in 5 ms means that the energy deposition in that time period is 10,000 or more times greater than the average of .0001 particle in 5 ms assumes that the mainstream scientific community thinks the energy is somehow delivered in a smoothed out fashion, a few eV at a time.
The assumption as best I can tell as an outsider is that one particle gives a chance of x (x Which is entirely reasonable, though no doubt oversimplified. But they also know that dose rates do make a difference, that alpha particles are many times more dangerous at a given energy because the energy is deposited in a short distance (high LET radiation as they call it) and that multiple hits might cause damage to great to repair and so forth. They're not idiots.
It just seems to me that you're assuming the whole community of radiation physicists and biologists is composed of incredible morons.
As for your model, I'd prefer to see it sketched out more, but of course you also have real life to worry about. And you'd be doing it for a somewhat skeptical audience.
Posted by: Donald Johnson at April 4, 2013 11:28 PMI must have deleted part of a sentence above. I meant to say the linear model assumes that if you absorb one particle of a given energy it gives a chance x of getting cancer and if you have two then the chance is 2x, etc.. Which seems reasonable if oversimpliifed, and so on
Posted by: Donald Johnson at April 4, 2013 11:35 PMDonald Johnson, thanks for your illuminating comments.
Posted by: Will Boisvert at April 5, 2013 12:43 AMLinear is different then affine. A linear equation must pass through the origin and thus a linear model would take a data point at a large dose and assume that the danger at zero dose is zero and draw a line. An affine equation is a linear equation with an affine offset (linear think y=mx and affine think y=mx+b).
Okay, this is easy to understand. In my experience "linear" always meant including the zeroth-order term, as in a first-order Taylor series expansion; just like "quadratic" always meant including the first-order and zeroth-order terms ... hence the confusion.
Posted by: Cloud at April 5, 2013 04:47 AMThis lineif the study had found an excess of 24% in mortality among nuclear workers, instead of a 24% deficit, the report would have been on CBS News.
tells me everything I need to know about Robert Park. He probably also thinks that Walter Cronkite lost the Vietnam War for the US, and that Dan Rather's report on Cesar Chavez and farm worker exploitation was paving the way for a Soviet takeover. He and my dad would get on just fine.
Nice rhetoric, but ad hominem. It's irrelevant to the question of whether there really was a connexion between the radiation and the dockworker mortality rate. (Although I'd be more interested in what happens to the guys in the engine room, seeing as I almost joined the Navy nuke program.)
I despair of all social-democratic causes when I see leftists reasoning that something must be wrong because conservatives believe it. "He sounds just like my dad ... and I don't get on with my dad ... so ..."
Posted by: Cloud at April 5, 2013 05:18 AMI despair of all social-democratic causes when I see leftists reasoning that something must be wrong because conservatives believe it. "He sounds just like my dad ... and I don't get on with my dad ... so ..."
If you don't understand the connection between a pro-nuclear stance and the specific mention of CBS News -- not ABC, not NBC, not just 'the news' -- and think that my making that connection has something to do with dislike of my father, then you just go right ahead and despair, and don't let the door hit your ass on the way out.
Posted by: NomadUK at April 5, 2013 08:17 AM@Donald Johnson, that what I'm telling you about the linear dose model is correct is obvious from the units (which measure energy, not power) and the manner in which doses are added. It's correct (well - not wrong for the reason discussed) for high doses, where energy and power are numerically identical. It's wrong for power. This is within my area of expertise, and I'm sure of it.
Simple example: the linear dose model tells me that I got alcohol poisoning because I drank five bottles of vodka. The truth is that I got alcohol poisoning because I drank five bottles of alcohol all at once. The first example relates to energy, the second to power.
As to the idiocy of the radiation physics community, there is some element of that. For instance: the paper which preceded Wing's (hence his is a "re-analysis") was written by Maureen Hatch, an epidemiologist then at Columbia. (She's now head of the Chernobyl Effects section at NIH, which tells you something about the quality of the information we receive in that regard.)
The Hatch paper is insanely stupid; I can't even describe it without raving. In addition to its idiocy, however, it also contains an error of fundamental physical fact on the first page so egregious that it's obvious that none of the authors or reviewers have any clue about basic undergraduate thermodynamics.
Beyond that, though, it's more subtle. Most of the story is the inertia invested behind a model applied far beyond its limits. The dose model for human effects arose in a big hurry, and out of necessary drew upon the applicable science available at the time. This happened to be the theory of cosmic ray interactions with inanimate matter. (Karl Morgan discusses this in his book "The Angry Genie".)
Moreover, in that same time frame HJ Muller published his work with X-rays demonstrating genetic damage in fruit flies. Genetic damage follows a linear model. This work became widely known around the time that the DNA mystery was unraveled, when the belief became widespread that genetics determines all.
So there was incredible inertia behind this understanding, and there were many outstanding successes.
But the human body is animate, and responds to stimuli; so the idea of using a model which tells you how many ionization events occur in a gas-filled tube upon which a cosmic ray impinges is kind of crazy.
And there's a difference between genetic damage, like double-strand breaks that can be seen and counted up, and health effects that arise fundamentally from chemical stress and the biological responses to it.
The scientists were doing all along what scientists are trained to do, which is to extend their model to new areas of investigation. But they didn't have the wisdom or the humility to stop at a point beyond which the model clearly is not applicable.
My opinion.
Also, @Walleby or @Walleye or @Whatever, way up there:
I adjusted the Wing data downward to reference zero dose, as I mentioned in the post. I do not believe I misunderstood the O/E data Wing presented.
As to the quality of the fit, I've certainly published fits to data in the scientific literature less good than this one, and been proud of the work. The fit is especially remarkable because actually it includes only one parameter: the linear scaling to the horizontal axis, which is necessary anyway because the doses measured are relative.
I agree the fit could be better, as it doesn't quite work out at low doses. Upon reflection, I believe this is easily explained if one considers that there is a pretty wide variation in radiosensitivity among the human population. The excess at very low doses then consists of people with the genetic or health misfortune to be unusually sensitive.
Posted by: Aaron Datesman at April 5, 2013 10:00 AM@ Aaron,
--“The linear dose model tells me that I got alcohol poisoning because I drank five bottles of vodka. The truth is that I got alcohol poisoning because I drank five bottles of alcohol all at once. The first example relates to energy, the second to power.”
Aaron, what you are talking about here is the concept of “dose rate”—the notion that a dose of radiation absorbed all at once will be more damaging than the same dose spread out over several days, months or years. Radiation epidemiologists do indeed pay very close attention to that and factor it into their dose models. That’s why consensus LNT models like the BEIR VII model include what’s called a DDREF, a dose-rate dependent risk factor.
You have misunderstood the implications of dose-rate for the issue of whether Linear Non-Threshold is an accurate model at low doses. Factoring in dose rate actually implies that LNT overestimates low-dose risks. That’s because LNT is based on data from the atomic bombings of Japan, where the vast majority of the radiation was absorbed in a brief flash of gamma and neutron radiation. (http://dels-old.nas.edu/dels/rpt_briefs/beir_vii_final.pdf) By contrast, low doses, especially those incurred during nuclear accidents, are typically absorbed over a much longer time period—days in the case of TMI, years in the case of Chernobyl and Fukushima.
So LNT assumes that low radiation doses spread over time are equivalent to the aggregate of those doses if they had been incurred all at once. In other words, it assumes that the radiation dose is taken in one huge swig of vodka, not many tiny sips spread out over months and years. But by your own vodka reasoning above, such a model must overestimate the risks of a given dose incurred at a low dose rate, not underestimate them.
That’s why at low doses LNT models factor in the DDREF, which is a departure from strict linearity. The DDREF at low doses is applied by dividing the cancer risk calculated from strict LNT by 1.5 or 2 depending on the model. But that means that the risk at low dose rates is judged to be smaller than what is calculated at high dose rates by strictly linear models.
Empirical findings clearly bear out the idea that lower dose rates are less harmful than higher dose rates for the same total dose. In radiation therapy for cancer, for example, the total radiation dose used is often huge and would kill the patient if given all at once. But when spread over the course of many weeks, the radiation doses are not lethal and indeed add only a modest extra risk of cancer, far outweighed by their effect in killing already cancerous cells.
Aaron, the assumption of strict linearity in dose-response models is indeed problematic and scientists wrestle with those problems (instead of ignoring them as you falsely insinuate.). But you get the implications of nonlinearity completely backwards. Virtually all proposals of non-linearity, including your own, logically imply that cancer risks from low-dose, and low dose-rate, radiation are smaller, not larger, than would be predicted by a strictly linear dose response extrapolated from high doses. You are barking up the wrong tree here.
--Aaron, if genetic damage caused by radiation exhibits a linear dose response, as you write, doesn’t that imply that cancer risk, which is an outcome of carcinogenic genetic mutation, also has a linear dose response? Perhaps not if there is a threshold for carcinogenesis, where a certain number of mutations must accumulate before a cell turns cancerous. But again, that implies a quadratic shape to the dose-response curve for cancer, which would therefore be sub-linear at low doses.
wvlgpujozsfwpmvujpo, mqpoyctpzn
Posted by: iaofjqdsgh at April 6, 2013 05:49 PMiaofjqdsgh:
Bad link.
Posted by: godoggo at April 6, 2013 06:01 PM


